Objectif DNB mathématiques
Des enseignants de mathématiques de l’académie de Créteil exposent ici certains dispositifs ou outils qu’ils pratiquent avec leurs élèves dans le cadre de la préparation au DNB. Il ne s’agit pas d’indiquer des « modèles » qu’il faudrait reproduire mais de fournir des exemples et des ressources à mieux partager.
Nous distinguons trois parties, qui se recoupent partiellement, selon que l’on prépare les élèves au fil de l’année de troisième, durant les périodes spécifiques des « brevets blancs » ou dans le cadre des révisions bilan de fin d’année.
I – Se préparer au DNB au cours de l’année de troisième
Préparer les élèves au DNB se pratique tout au long de l’année de troisième. Il est essentiel que les élèves soient exposés régulièrement à des fragments de l’épreuve, sous forme d’exercices partiels ou d’exercices corrigés sur lesquels ils peuvent s’entraîner toutes l’année.
Nous vous proposons ici quatre ressources qui peuvent être exploitées toute l’année :
- la banque de ressource BAREM du ministère pour accéder à des parcours de révision des notions principales du programme de mathématiques ;
- l’outil de vie scolaire « Pronote » pour constituer des QCM de révision et les communiquer aux élèves ;
- un « exerciseur » comme « Labomep » pour élaborer ou utiliser des parcours d’entraînement automatisés, adaptés aux besoins des élèves ;
- un jeu de plateau, « Algebra Quizz », pour travailler le calcul littéral de façon ludique !
1. Utilisation de BAREM (Banque de Ressources pour Enseigner les Mathématiques) pour créer des modules de préparation au DNB
Cyril MICHAU et Nicolas LEMOINE
Le groupe académique de réflexion sur l’enseignement des mathématiques au collège mettra à disposition un espace dédié à la révision du brevet sur les Banques de Ressources Numérique Educatives proposées par le ministère. Tous les thèmes du programme de mathématiques seront abordés.
Les BRNE
Les BRNE sont un espace accessible à l’ensemble des professeurs au niveau national, un article sera proposé sur Eduscol, le portail mathématique national ainsi que dans les BRNE directement. Cet article mentionnera l’existence de cet espace dédié aux élèves dont l’objectif est de réviser le brevet.
Côté enseignant, il sera possible de proposer ces ressources à ses élèves en suivant leurs résultats, ou bien d’être simplement « consommateur » et de laisser les élèves les utiliser en autonomie. Il sera possible aussi pour les professeurs de s’approprier ces modules qui seront créées afin de les personnaliser (en y ajoutant leur propre ressources ou en modifiant les ressources proposées par exemple).
Côté élèves : nous fournirons des liens qui mèneront directement aux modules pour que les élèves puissent travailler les notions de leur choix.
Les modules
Il s’agira d’un enchainement de « granules » avec correction automatique. Ces granules peuvent être une vidéo qui traite de la notion, un QCM, un exercice interactif ou encore une tâche à prise d’initiative. Le format sera relativement court pour chacun des modules ; il y aura tout au plus 4-5 graines à l’intérieur.
Exemple :
1. Présentation de la notion (extrait de cours) ;
2. Vidéo de moins de 3 minutes qui explique la notion avec un exemple ;
3. Un QCM d’application directe ;
4. Un exercice un peu plus poussé où l’élève rédige la réponse dans une zone de texte libre ;
5. Une tâche à prise d’initiative ou encore un exercice de brevet.
Les ressources seront accessibles par un lien sur les BRNE, ou en tapant [REVBREVET] dans la barre de recherche. Nous fournirons également des liens directs vers les ressources (classées par thématique).
Exemple : « Calcul de longueurs dans le triangle rectangle » :
https://edu.tactileo.fr/go?code=5DLV
L’objectif est de fournir une base de données d’exercices auto-corrigés aux collègues ou élèves. Chaque collègue pourra l’utiliser telle quelle ou bien approfondir son utilisation en se l’appropriant.
Ces parcours peuvent être utilisés en classe pour favoriser la différenciation des révisions. Ils peuvent aussi être proposés hors la classe.
Cette base s’appuiera également sur un service fourni par le MEN dans le cadre du plan numérique lancé en 2016, les banques de ressources éducatives (BRNE).
La diffusion se fera par la plateforme nationale des BRNE, par le compte twitter national de mathématiques (@eduscol_maths) ; ainsi que par le portail national de mathématiques.
2. Réviser le DNB à l’aide de QCM sur « Pronote »
Martine BRUNSTEIN
Professeure au collège DU PARC
94 SUCY-EN-BRIE
Utilisation des ressources numériques utilisées dans l’ENT de l’établissement
L’établissement ayant fait le choix de Pronote,les élèves sont habitués à se connecter régulièrement pour consulter toutes les informations relatives à leur classe (les notes,les compétences, les devoirs à faire, les travaux à déposer numériquement…).
Tout au long de l’année des QCM sont proposés aux élèves pour réviser une notion,préparer un contrôle, vérifier les automatismes d’une leçon à acquérir… Au fil du temps, et après un temps d’adaptation des élèves, ils sont devenus réguliers.
A l’approche de la date du DNB et dans le cadre des révisions, ils peuvent être également utilisés. Le support numérique paraissant parfois moins contraignant pour certains élèves.
Un QCM peut être créé et proposé aux élèves :
- pour réactualiser la leçon avant une séance de révision sur un thème donné et on proposera alors des exercices type brevet sur le thème ;
- pour réviser des automatismes à maitriser dans un thème précis.
Un QCM peut être un support pour :
- un travail de préparation avant une séance avec le professeur ;
- un entrainement individuel et personnel à distance ;
- un entrainement pour une séance de révision collégiale ou en groupe.
Un QCM comporte des questions basiques de façon que tous puissent faire le lien avec une leçon et puissent également répondre rapidement. L’élève a accès à un corrigé à la fin ou à la fin de chaque question et peut indiquer s’il a trouvé cela facile ou non.On peut y associer des textes , des images, des vidéos…..
On choisit les modalités de passation (ordre aléatoire des questions,des réponses, temps limité ou pas …). Dans le cadre de révisions, le QCM ne sera pas évalué.
On associe directement le QCM au cahier de textes.
Page d’accueil des QCM

Menu clic droit à partir du nom du QCM

Menu clic droit à partir des questions du QCM

Dans certaines épreuves du brevet, les élèves doivent parfois répondre à un QCM. Cet entrainement permet aussi de refaire avec un eux un peu de méthodologie face à un exercice de mathématiques de ce type : se munir d’un papier, d’un crayon, de sa calculatrice et s’intaller en posture de recherche sans avoir le souci ou la contrainte de la rédaction écrite.
Le professeur a un récapitulatif des résultats obtenus par les élèves ; cela peut donc servir aussi d’évaluation diagnostique avant une séance de révision.
Enfin on trouve de nombreux tutoriels sur les QCM de Pronote sur Internet qui aident à leur utilisation et à leur création. La prise en main est assez facile.
Dans Pronote existe également une bibliothèque de QCM édités par Nathan et en consultation libre. Comme pour ses propres QCM, on peut les modifier et les utiliser à sa guise.
En documents joints voici des exemples de QCM déjà utilisés pour des préparations contrôles ou de DNB blanc ou qui vont être utilisés en révision avant l’épreuve du mois de juin.
3. Réviser le DNB en mathématiques avec Labomep
Fabienne GLEBA
Professeure au collège DE LATTRE
94 LE PERREUX-SUR-MARNE
https://labomep.sesamath.net/
Inscriptions sur Labomep
Une fois la structure de l’établissement renseignée, le professeur peut inscrire ses classes (via l’ENT, en utilisant un fichier Sconet ou un fichier tableur). Il peut aussi demander aux élèves de créer leur compte (à autoriser dans les préférences de l’établissement) qu’un formateur devra valider.
Une documentation Labomep est disponible sur : http://www.labomep.net/fiches/faq.php
Séances de préparation au brevet
Des séances de révision sont proposées, notamment avant les brevets blancs, sur la plateforme Labomep. Cet exerciseur propose de nombreux exercices et animations interactives. Les questions sont corrigées automatiquement au fur et à mesure de la progression du travail de l’élève ce qui lui permet une auto-évaluation. Il a aussi la possibilité de visionner des aides animées, d’utiliser un tableau de conversion, une calculatrice.
Le thème des séances de révision est indiqué, chacune contient quatre exercices en moyenne ainsi que des animations interactives de rappels de cours ou de méthodes concernant les notions abordées dans le thème. On peut aussi intégrer un QCM récapitulatif.
Les élèves ont l’obligation de faire deux exercices de chaque séance avant une date butoir. La plupart des élèves font tous les exercices.
Ils peuvent faire plusieurs fois une même séance (entière ou un exercice en particulier) au cours de l’année (les séances restent accessibles tout au long de l’année).
Plusieurs organisations ont été testées :
- mettre en ligne une séance par semaine pendant 6 semaines ;
- mettre en ligne en même temps les 6 séances, 6 semaines avant le brevet blanc.
Les élèves ont plutôt plébiscité la seconde organisation.
En fonction des demandes des élèves, des séances peuvent être données « à la carte ». On peut pour cela utiliser des corrections animées d’exercices ou des exercices interactifs du DNB.
Exemple d’arborescence
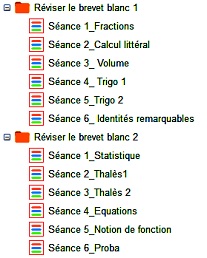
Exemple d’une séance de révision sur le théorème de Thalès
(Les flèches vertes indiquent les animations interactives, qui donnent des rappels de cours et de méthodes).

Liste des QCM récapitulatifs

Exemples d’animations interactives

Pour les élèves qui le souhaitent, en collaboration avec la documentaliste, des créneaux sont proposés au CDI aux élèves de troisième afin qu’ils avancent leur travail. Le professeur peut suivre l’avancée des séquences et des résultats et peut prévoir une remédiation sur certains thèmes avec certains élèves en classe. Il peut aussi rajouter une séance sur un thème spécifique à certains élèves, parfois sur leur demande. Des élèves en retard sur le travail peuvent également se voir proposer un créneau au CDI pour faire le travail.
4. « Algebra Quizz » : travailler le calcul littéral en jouant
Alberto AHUMADA
Collège ROGER MARTIN DU GARD
93 EPINAY-SUR-SEINE
Alberto Ahumada nous propose ici un jeu « clé en main » permettant de travailler un sujet souvent difficile et a priori austère, le calcul littéral. N’hésitez pas à l’expérimenter, vous aurez peut-être la surprise de voir vos élèves se prendre au jeu.
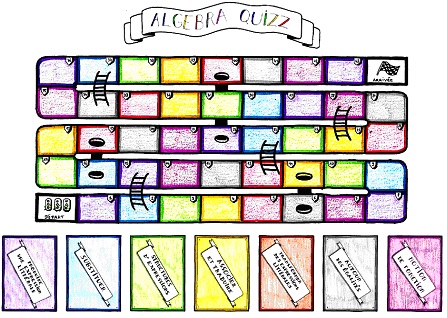
Plateau et règles du jeu :
Objectif :
Arriver le premier à la fin du parcours.
Nombre de joueurs :
De 2 à 4 joueurs.
Déroulement d’une partie « classique » :
• Les joueurs installent leurs pions sur la case départ, mélangent les cartes de chaque catégorie et les disposent face cachée à proximité du plateau de jeu.
• Les joueurs lancent à tour de rôle le dé et celui ou celle qui obtient la valeur la plus grande commence la partie.
• A tour de rôle, chaque joueur :
– lance le dé et avance du nombre de cases correspondantes puis tire une carte de la couleur de la case ;
– si le joueur répond juste alors il pourra lancer le dé au prochain tour ;
– si le joueur ne parvient pas à répondre à la question alors il reste sur la même case et devra au tour suivant à nouveau tirer une carte de la même couleur, et ce, jusqu’à ce qu’il donne une réponse juste.
Cartes et réponses :
II – Préparation et exploitation des DNB blancs
Les « brevets blancs » sont des moments privilégiés de préparation des élèves au DNB.
Il est indispensable de ne pas totalement externaliser, hors la classe, les temps de révision. Il faut prévoir des moments d’accompagnement, notamment méthodologique, des révisions des élèves au sein de la classe, dans le cadre de l’accompagnement personnalisé par exemple. On peut par exemple faire élaborer des fiches méthode ou des résumés de cours, notamment sous forme de cartes mentales.
On peut concevoir pour ses élèves (ou avec ses élèves) un guide de révision très explicite, un programme de travail qui aide les élèves eux-mêmes et aide aussi ceux qui les accompagnent (parents, associations, professionnels dans le cadre de « Devoirs faits »…) : voir à ce propos l’exemple du « Cahier de révision » présenté ci-après.
Pour tirer le meilleur parti des brevets blancs, le moment de la correction est essentiel. Il s’agit, pour le professeur, d’expliciter ce qui permettra de progresser et, pour l’élève, d’apprendre de ses erreurs. On peut faire corriger une partie des exercices par les élèves, par exemple en groupes, ou travailler sur des extraits de copies d’élèves, analyser différentes réponses, justifier les réussites, nommer les erreurs, les classer, y remédier ensemble.
Les épreuves blanches ont pour objectif de faire progresser les élèves, de les aider à se mobiliser, de restaurer, autant que faire se peut, leur confiance en eux. Tout ce qui concourrait au résultat inverse, et particulièrement des notes catastrophiques, serait à repenser. Le « brevet blanc » doit être pensé et vécu comme une évaluation formative avant tout. On peut donc s’autoriser à aménager l’épreuve si nécessaire (les élèves sont particulièrement réceptifs à ces moments là) :
- répondre à une ou deux questions pour éviter qu’un élève ne se décourage ;
- rappeler au tableau certains points méthodologiques (gestion du temps, lecture de tout l’énoncé…) ;
- autoriser une fiche méthode personnelle ou résumé de quelques notions ;
- prévoir une salle particulière pour les élèves en très grande difficulté dans laquelle ils pourraient recevoir une aide particulière.
1. Des QCM « Google Form » de préparation au brevet blanc
Geoffroy LABOUDIGUE
Collège ROGER MARTIN DU GARD
93 EPINAY-SUR-SEINE
Des QCM de révision au DNB blanc sont proposés aux élèves hors la classe, sous forme de Google Form. Le lien suivant en donne un exemple (version élève).
https://docs.google.com/forms/d/1vTP5_e9ruoc__VC-Sb4aGcZQfqtxd4_6kZzpx-WMi7M/edit?ts=5aa5902d
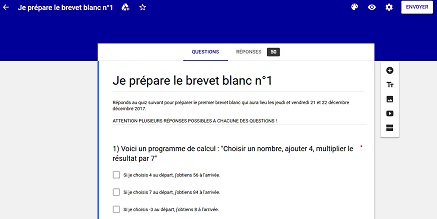
Ces QCM sont systématiquement proposés aux élèves, hors la classe, avant les brevets blancs. Un retour statistique individualisé permet d’organiser les séances de révision en classe selon les besoins des élèves.
Document pdf de prise en main de Google Form réalisé par Geoffroy LABOUDIGUE :
2. Le « cahier de révision » des brevets blancs
Alberto AHUMADA
Collège ROGER MARTIN DU GARD
93 EPINAY-SUR-SEINE
Avant chaque brevet blanc, un « cahier de révision » permet aux élèves de réviser à l’aide d’exercices d’entraînement correspondant aux capacités attendues et fournit des conseils méthodologiques et organisationnels.
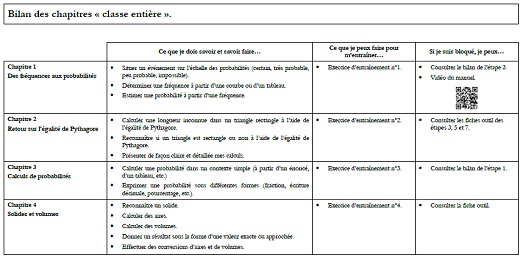

Après le brevet blanc, le cahier est complété dans le cadre de la correction personnalisée des copies.
Sujets de brevet blanc et cahiers de révision du collège ROGER MARTIN DU GARD.
3. Élaboration de sujets de brevets blancs et d’activités d’entraînement
Il convient de veiller à la progressivité des exercices dans les brevets blancs et entre le premier brevet blanc et le deuxième. Le premier brevet blanc, tout particulièrement, doit faire appel à des connaissances et des compétences variées et ne pas, par exemple, cibler trop exclusivement un domaine pour des raisons de difficultés de progression commune.
Des professeurs proposent ici des activités pouvant notamment servir d’entraînement aux brevets blancs ou en constituer des exercices.
Loïc ASIUS
Collège LIBERTÉ
93 DRANCY
Des exercices d’algorithmique et programmation avec Scratch :
Une tâche intermédiaire « Vitesse sur les routes » :
Une tâche intermédiaire « Tétris et transformations » :
Hela BENSALAH
Collège Erik SATIE
77 MITRY-MORY
Un ensemble d’exercices « Machines à café » :
III – Révisions de fin d’année
Les établissements organisent généralement une semaine (voire davantage) de révision des épreuves écrites du DNB à destination des élèves de troisième. Nous indiquons ci-dessous un exemple d’organisation permettant de travailler en groupes de besoins à effectifs réduits. Nous donnons enfin un exemple d’alternance des formes et des contenus susceptible d’instaurer une dynamique de réussite.
1. Un exemple d’organisation permettant d’impliquer l’ensemble des professeurs de mathématiques
Zouhir EL AMRI
Collège FEDERICO GARCIA LORCA
93 SAINT-DENIS
L’organisation des révisions de fin d’année pour les élèves de troisième de notre établissement permet à l’ensemble des professeurs de mathématiques du collège d’être à 100 % de leur temps de service hebdomadaire mobilisés pour cela. Ceci nous permet de prévoir des groupes à effectifs réduits correspondant aux besoins des élèves.
Les dates
Il est envisagé cette année d’organiser les révisions de fin d’année du lundi 11 juin au mercredi 27 juin 2018 (deux semaines et demi), sur une période plus longue que l’an passé.
Les Horaires
Comme les années précédentes, les horaires changeront pour les troisièmes : deux créneaux d’une heure vingt et un créneau d’une heure trente par jour (français-mathématiques-histoire et géographie), 9h - 10h20 puis 10h40 - 12h puis 14h - 15h30 (pas de récréation l’après-midi pour eux). Le mercredi et le vendredi seront consacrés aux sciences et technologie sur un dispositif identique mais qui sera affiné suite aux remontées des équipes concernées.
Les autres niveaux (sixième, cinquième et quatrième) bénéficieront eux d’emplois du temps aménagés et seront pris en charge en EPS, arts plastiques, éducation musicale, anglais, LV2, formation SST, un peu Physique-chimie-SVT-technologie, des sorties pédagogiques, avec des horaires augmentés pour certains enseignants (ceux de ces disciplines n’ayant plus de troisièmes en charge sur cette période).
Possibilité sera donnée aux élèves d’une prise en charge par des assistants pédagogiques sur les créneaux 15h30 - 17h pour les élèves volontaires souhaitant poursuivre les tâches entamées en classe.
Cela donne côté élèves : 4h10 de cours par jour les lundis, mardis, jeudis et vendredis, 2h40 le mercredi ; donc 19h20 au total.
Cela donne côté enseignants de français, mathématiques et histoire-géographie : 9h-12h puis 14h-15h30 les lundis, mardis et jeudis, avec une pause de deux heures ; donc 13,5h au total au lieu de 16,4h en REP+.
Et cela donne côté enseignants physique-chimie-SVT-technologie : 9h-12h les mercredis, 9h-12h puis 14h-15h30 les vendredis ; donc 7,5h au total (les 6h restant permettront les prises en charge d’autres niveaux afin d’équilibrer à 13,5h comme ceux de français, mathématiques et histoire-géographie).
Protocole de création des emplois du temps
Les 5 classes de troisièmes sont réparties en trois grands groupes. Pour chacune des matières concernées, dans chacun de ces trois grands groupes, 7 sous-groupes de français, 7 sous-groupes de mathématiques et 4 sous-groupes d’histoire-géographie sont créés (cela correspond ici aux nombres de professeurs qui interviendront dans le dispositif, ils pourront être modifiés si nécessaire avec par exemple l’intervention d’assistants pédagogiques et/ou d’enseignants de physique-chimie-SVT-technologie). Ces sous-groupes sont des groupes « de niveau » (faible/moyen/bon), ou « de besoins » pour chaque matière. Ils sont construits sur la base des résultats des brevets blancs. Cela correspond donc à 54 sous-groupes ((7 + 7 + 4) × 3 ou 18 × 3). Le modèle repose donc sur une permutation circulaire de ces trois grands groupes sur les trois matières dans les trois créneaux de la journée. Idem pour les enseignants de physique-chimie-SVT-technologie. Chaque élève ayant des emplois du temps personnalisés.
Contenu des séances
Liberté est laissée aux enseignants. La méthodologie est en fil directeur. Il faudra aider chaque élève à réussir au mieux face à un sujet. Le message : « Prenez des initiatives ! Écrivez ! Battez-vous sur un sujet ! ». En mathématiques, les supports sont adaptés en fonction des niveaux.
2. Un exemple de contenus pour 7 séances de révision
Thierry ICHELMANN
IA-IPR de mathématiques
Nous proposons ici un exemple possible d’un travail de 16h avec les élèves de troisième, en préparation à l’épreuve de mathématiques du DNB.
En fonction du temps disponible et de l’organisation de l’établissement, la mise en œuvre peut être adaptée.
Proposition : 5 séances de 2h et 2 séances de 3h.
Séance 1 : Révisions sur les 5 thèmes du programme
Utilisation de QCM thématiques pour réviser les 5 thématiques du programme (utilisation possible de diaporamas, « Plickers », Google Form, Pronote, Labomep…).
10 QCM de 5 questions.
Thème A : Nombres et Calculs
Thème B : Organisation et Gestion de Données – Fonctions
Thème C : Grandeurs et Mesures
Thème D : Espace et Géométrie
Thème E : Algorithmique et programmation
Séance 2 : Point sur l’intégration des compétences de base
Utilisation d’extraits de sujets de DNB (notamment de la série professionnelle) de sessions précédentes afin de vérifier et de consolider l’intégration des compétences de base du programme.
Séance 3 : Travail ludique sur les compétences algébriques du programme du cycle 4
Utilisation d’un jeu de cartes fourni (et d’une proposition d’utilisation) afin de se familiariser et d’augmenter son degré de maîtrise des compétences algébriques du programme.
Séance 4 et 5 : Travail méthodologique et spécifique d’extraits de sujets de DNB
Aide au développement de questionnements et de méthodes appropriés à la réussite des épreuves de DNB.
Travail sur des extraits de sujets de DNB et aides à la résolution (coups de pouce).
Ci-dessous est donné un une activité d’apprentissage progressif d’un exercice de DNB « Séjour au ski » (Amérique du Nord 2016).
Séance 6 et 7 : Entrainement sur des sujets inédits de type DNB
Entrainement sur des séances de deux heures de type DNB, suivi d’un point récapitulatif (point méthodologique, analyse sujet, compétences visées, éléments de réponse, points de vigilance).
Remarque : séance préalable
Avant ce temps spécifique de révision, un travail récapitulatif sur certaines compétences de base peut être réalisé, avec des outils comme « le cahier de révision », et énoncé et éléments de corrigé d’un sujet blanc de DNB, les supports sont fournis.

