La symétrie axiale
Dans l’apprentissage de la symétrie au collège (dans tout ce texte lorsque le mot symétrie est, à tort, employé seul il signifie réflexion ou symétrie orthogonale), on ne peut plus se contenter de l’observation et de l’action. L’utilisation des propriétés pour agir constitue l’essentiel des apprentissages. Mais en ce qui concerne les élèves en grande difficulté, bénéficiaires des actions de remise à niveau, les priorités se situent en amont :
– la maîtrise et parfois l’utilisation de base des outils de dessin ;
– la vérification, l’entretien et la capacité à mobiliser les acquis de la plupart des enfants arrivant en 6ème tels que : compléter un dessin plus ou moins figuratif par symétrie par rapport à un axe vertical, trouver au moins un axe de symétrie dans une figure qui en possède ;
– la mobilisation de notions utiles telles que droites perpendiculaires, milieu d’un segment .
Des activités préparatoires aux acquisitions de 6ème, peuvent être mises en place à la fois en cycle des approfondissements de l’école élémentaire et en cycle d’adaptation du collège : pliages, piquages, dessins à main levée, observation de monuments ou de jardins à la française etc.
Les difficultés rencontrées par les élèves sont comme souvent de natures différentes. Entre autres,
– celles qui sont liées au vocabulaire, et qui doivent faire l’objet d’un apprentissage pour l’ensemble de la classe : elles ne seront pas traitées dans ce document dédié à la remise à niveau ;
– celles qui sont liées à la précision des constructions et à la place de l’axe par rapport à la figure, qui doivent absolument être traitées dans le cadre de la remise à niveau. Des pistes sont proposées dans ce document.
Dossier réalisé par :
Nicolas BRAY, Catherine BRUNET, Marie-José HOUSSIN, Denise MAHIEU, Francine MARTEIL, Alexandre SIDIN, Roland VENTRE, Anne VOLTOLINI.
La partie A est en ligne
l’intégralité du document est téléchargeable en bas de page.
Plan du document :
A-La symétrie dans les évaluations : des outils d’identification et d’analyse d’erreurs.
III- Objectifs de la classe de sixième.
B-Reconnaissance et tracés de droites perpendiculaires : des préalables au travail sur la symétrie.
I Diagnostic
II Remise à niveau
III Quelques exemples de programmes de construction (en rapport avec les tracés de perpendiculaires)
C-Quelques exercices à propos de milieu
milieu dans le langage naturel
milieu en mathématiques
D-Quelques activités autour de " Axes de symétrie " et " Compléter une figure par symétrie "
les gabarits mobiles
jeux de miroirs
pliage et octogone régulier
" plier-déplier "
mosaïque
E-En prolongement, quelques activités sur la symétrie elle-même
le chat
la tulipe
le moulin
F-Remarques sur l’utilisation des outils de construction
G-Pour avoir d’autres idées.
La symétrie dans les évaluations
I- La symétrie.
1. Comparaison 6ème / CE2
En 1997, l’exercice suivant a été proposé dans les évaluations en CE2 et en sixième (même consigne et même figure). 55,8 % des élèves à l’entrée en CE2 arrivent cette année là à obtenir un tracé exact et complet (à la règle ou à main levée). Il a été à nouveau proposé en CE2 en 1998 et la prise d’information étant plus complète nous en détaillons les scores.
En CE2 (1998)
56% des élèves réussissent un tracé exact
3,4% reproduisent par translation
9,4% respectent la forme générale de la figure mais pas la distance à l’axe
29% font un tracé inexact non repéré par les autres codes.
En 6ème (1997)
92,1% des élèves réussissent un tracé exact
7,3% donnent une autre réponse
0,6% non -réponse
Complète le dessin comme si tu pliais la feuille en suivant le grand trait.
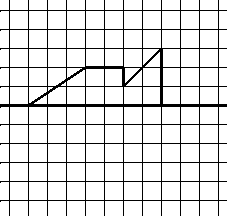
Il s’agit de compléter par symétrie axiale une figure dessinée sur quadrillage, l’axe étant horizontal, la figure au-dessus de l’axe. C’est la situation la plus rencontrée à l’école primaire et donc la mieux maîtrisée.
Mais le quadrillage n’est pas symétrique par rapport à l’axe (5 carreaux au dessus contre 7 en dessous). C’est une situation difficile en CE2. Cette difficulté persiste en début de sixième, elle sera donc à repérer. Par contre, on notera que le même exercice donné en début de sixième indique de très nets progrès, ce qui permet de pointer les élèves de chaque classe en grande difficulté. La remise à niveau en sixième permettra de travailler avec les deux élèves d’une classe (les 7,9%) qui ne réussissent pas ou qui ne font pas l’exercice en début d’année.
A l’école depuis le CE2, tout un travail a été fait sur la position horizontale ou verticale de l’axe et sur la position de la figure par rapport à l’axe, droite gauche, au-dessus, en dessous, touchant l’axe ou non.
Mais les activités sont essentiellement réalisées sur papier quadrillé ou pointé. Au cours de ces activités, on a pu faire émerger quelques propriétés (conservation de la forme et de la taille ) mais il n’est pas question à l’école de faire un travail systématique sur ce sujet.
En sixième, on développera donc ces connaissances. Par ailleurs l’utilisation progressive de lettres pour désigner les points de la figure permettra aussi de mieux communiquer.
2. Complexité de la tâche
Complète le symétrique de la figure par rapport à la droite tracée en gras.
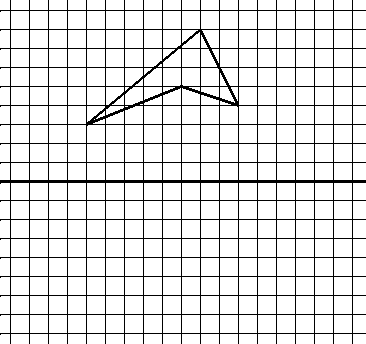
Pour cet exercice, proposé à l’entrée en sixième et malgré la similitude apparente des tâches avec celles de l’exercice précédent, on observe que les scores chutent de façon très significative.
32% des élèves réussissent exactement la figure symétrique.
0,5 % donne une réponse partielle mais sans élément erroné
8,2% font une figure retournée et superposable à la figure de départ mais mal positionnée (code 5)
10,9% font une figure fausse mais l’idée du retournement est présente (code 6)
30,5% obtiennent une figure en translatant ou en essayant de translater
7,4% donnent une autre réponse fausse
10,4% des élèves ne répondent pas.
Dans cet exercice, le non-respect de l’équidistance à l’axe est aussi repéré dans cet item par le code 5.
On peut penser que la tâche étant plus complexe, en partie à cause de l’éloignement de la figure et de l’axe, l’élève n’associe plus la symétrie à l’idée de retournement. En outre, il semble que la position verticale ou horizontale de l’axe dans le cas d’une figure moins usuelle (cette figure peut sembler inhabituelle car le quadrilatère possède un angle rentrant qui " gêne " l’élève) induise davantage l’idée de translation.
Finalement, seul un petit tiers des élèves à l’entrée en sixième réussit cet exercice !
A l’aide du quadrillage trace le symétrique de cette figure par rapport la droite d.
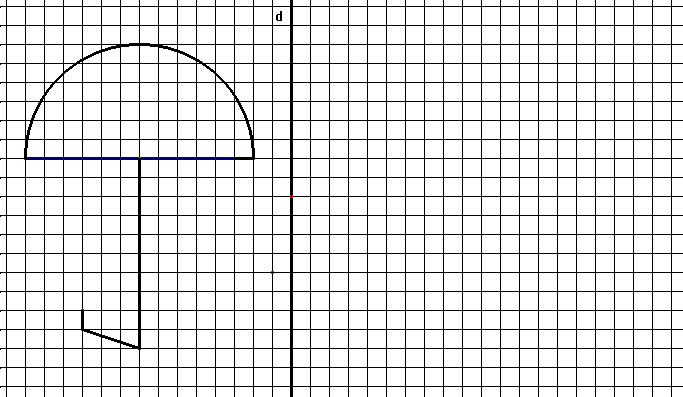
Cette année-là, on peut comparer ces scores à l’exercice du " parapluie ", figure proposée avec un axe vertical situation familière à l’école mais en fait assez difficile car les propriétés de la symétrie doivent être utilisées et la figure suffisamment analysée.
62,6% arrivent à tracer le demi-cercle au bon endroit et avec un rayon juste .
33,4% placent convenablement le manche par rapport à la droite d, la poignée étant bien tournée et les longueurs justes.
Trace, en couleur, l’axe ou les axes de symétrie de chaque figure.

A la rentrée 1999, l’exercice suivant demandait à l’élève entrant en sixième de reconnaître un ou des axes de symétrie de trois figures dessinées sur quadrillage.
Il s’agissait de repérer les compétences de certains élèves sur l’image mentale d’un axe de symétrie.
Les scores de réussite sont faibles mais il faut rappeler ici que le " tracé d’un ou des axes de symétrie des figures suivantes : triangle isocèle, triangle équilatéral, losange, rectangle carré. " est une compétence exigible de fin de sixième !
Pour le rectangle,
38,1 % des élèves dessinent les deux axes d’un rectangle
10,4% en dessinent un seul sans élément erroné
12,4 %dessinent une ou deux diagonales
17,7% dessinent les médianes et une ou deux diagonales
7,7% ne répondent pas
13,7% proposent une autre réponse
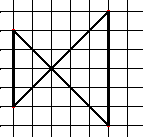
Pour la seconde figure,
39% dessinent l’axe attendu
4,4% tracent la droite verticale passant par le sommet commun aux deux triangles
15,7% ne répondent pas
17,1% proposent une autre réponse.
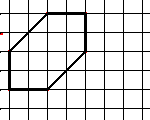
Pour la dernière figure, 36,1% dessinent les deux axes12,5% dessinent un seul axe sans aucun élément erroné8,8% ne répondent pas42,5% proposent une autre réponse
En conclusion, : Pour mieux faire comprendre la symétrie axiale, poursuivre les activités de pliage et de piquage, et utiliser le papier calque ou le miroir, s’avère indispensable et ceci tant que l’image mentale de la symétrie n’est pas stabilisée.
De même, il est absolument nécessaire de demander encore en sixième des dessins à main levée, sur tout support y compris sur papier blanc. C’est un préalable aux exercices de constructions fines avec les instruments sur papier blanc ainsi qu’aux exercices mettant en jeu un axe oblique coupant ou non la figure, qui font appel aux objectifs de fin de 6ème.
1- Reconnaissance de la position relative des droites
On doit penser à compléter les observations sur la symétrie par celles qu’on peut tirer des items relatifs aux droites et à leur direction, c’est-à-dire à la reconnaissance de droites parallèles ou perpendiculaires.
La non maîtrise du vocabulaire est une source de difficultés (code 5).
Les élèves qui associent perpendiculaire à verticale et parallèle à horizontale ou à non sécante sur le dessin en est une autre (code 6).
D’autres élèves conçoivent aussi la perpendicularité comme une propriété intrinsèque à une droite ce qui peut contribuer à expliquer l’importance du taux des autres réponses (code 9).
6ème - 97- Item 22 (reconnaître une droite perpendiculaire à la droite (d))
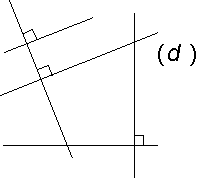
60,1 % donnent une réponse exacte.
2,4% dessinent une autre droite perpendiculaire à (d).
5,7% colorient la droite parallèle à la droite (d) (code 5).
10,4% colorient la verticale (code 6).
1,9% colorient deux droites perpendiculaires mais (d) n’est pas l’une d’entre elles.
16,5% donnent une autre réponse.
3% ne répondent pas.
Il est à noter qu’à l’item consistant à reconnaître sur la même figure une droite parallèle à (d) 4,6% colorient une droite perpendiculaire à la droite (d) et 4,3% colorient l’horizontale.
2— Tracer une droite perpendiculaire.
Trace la droite perpendiculaire à la droite (d) et qui passe par le point C
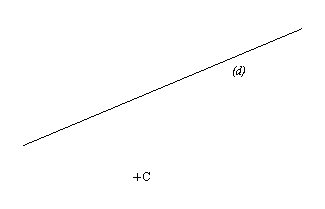
60,6 % tracent la perpendiculaire à D passant par le point C (au degré près).
1,1% trace une perpendiculaire à D mais qui ne passe pas par le point C.
28,6 % tracent une droite passant par C mais non perpendiculaire à D.
6,6 % donnent une autre réponse.
3,1 % ne répondent pas.
Il s’agit d’utiliser convenablement l’équerre mais en tenant compte de deux contraintes et cela demande donc aux élèves de s’organiser.
Il est à noter que plus du tiers des élèves ( 38,3 %) entrant en sixième se trouvent en difficulté sur cet exercice.
3- Placer le milieu d’un segment.
6ème - 97 - item 76. Placer le milieu d’un segment.
On donne quatre points A, B, C et D.
Trace les côtés du triangle ABC.
Marque le milieu du segment [AD], appelle J ce point.
Trace le segment [JB].
74,6 % placent et nomment correctement le milieu.
3,7 % placent correctement le milieu mais ne donne pas de nom.
9,2 % placent mal le milieu mais le nomme correctement.
5,8% donnent une autre réponse.
6,7% ne répondent pas.
Plus d’un élève sur cinq (21,7 %) ne parvient pas, dans cette situation, à placer le milieu du segment [AD] d’extrémités données. On peut supposer que le score aurait été un peu plus élevé si la figure avait été réduite au seul segment [AD]. En effet certains abstentionnistes auraient alors sans doute répondu, et ceux qui ont placé le milieu d’un autre segment auraient sans doute bénéficié du manque de distracteurs.
III- Objectifs de la classe de sixième.
Et en fin de sixième, où en est-on ? (Etude des évaluations de fin de sixième. (DEP- APMEP))
[DEP : Direction de l’Evaluation et de la Prospective
APMEP : association de professeurs de mathématiques de l’Enseignement Public]
Au programme de sixième.
Compétence exigible : " construire le symétrique d’un point d’une droite, d’un segment, d’un cercle, que l’axe de la symétrie coupe ou non la figure ".
a- La prégnance de la verticale et de l’horizontale reste importante.
6ème - EVAPM 6 / 97-
Construire, avec un axe oblique, le symétrique d’un point extérieur à l’axe ou d’un segment dont une extrémité est un point de l’axe.
62 % des élèves maîtrisent la construction du point
56 % la construction du segment horizontal.
59 % la construction du segment vertical.
19% De nombreux élèves prolongent le segment. En fait, ils appliquent une symétrie centrale dont le centre est le point d’intersection du segment et de l’axe. (19% pour le segment horizontal, 11% pour le segment vertical).
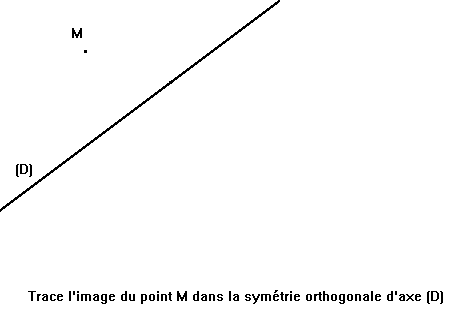
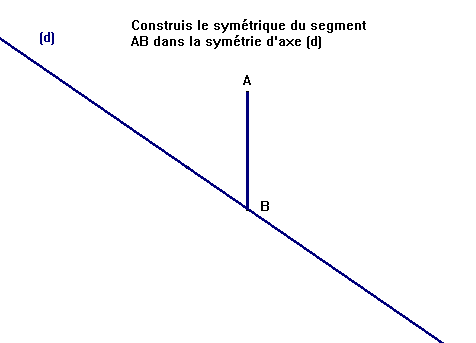
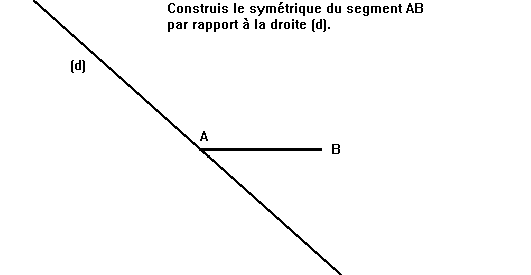
Les compétences en symétrie sont encore assez fragiles en fin de sixième et les difficultés rencontrées par les élèves dans l’utilisation des instruments est une explication à cette fragilité.
Par ailleurs, les évaluations de l’APMEP montrent que, en cinquième, les constructions liées aux symétries (axiale et centrale) ne provoquent pas plus de difficultés que les autres constructions.
b- Cas de l’axe qui coupe la figure ou qui fait partie de la figure
EVAPM6/97 (Fa)
Trace le symétrique de la figure ci-dessus dans la symétrie orthogonale d’axe (d).
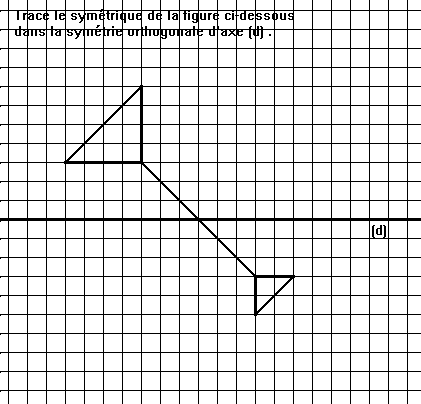
L’activité est à support quadrillé, l’axe est horizontal et il coupe la figure : un peu plus d’un élève sur deux (59%) réussit mais 12 % des élèves ne répondent pas.
Fin de 6ème- DEP 94 - exercice 26. Item a
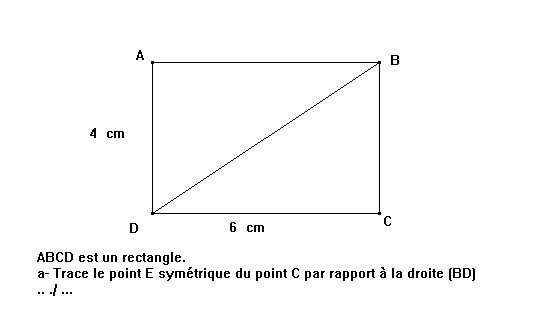
ABCD est un rectangle, il est dessiné ainsi que le segment [BD].
La première question demande de construire le point E symétrique du point C par rapport à la droite (BD)
37,9 % placent le point E correctement.
43,1 % donnent une autre réponse.
19,0% ne répondent pas.
62 ,1 % n’arrivent pas à la construction du point E.
Il s’agissait de comprendre l’énoncé, puis d’isoler l’axe de la symétrie de la figure (appel au concept de la droite car seul le segment est dessiné) et de construire le symétrique du point demandé.
On peut aussi lier cet exercice aux représentations des axes de symétrie du rectangle chez les élèves. De nombreux élèves (et encore au delà de la sixième) perçoivent les diagonales comme des axes de symétrie du rectangle, donc plus tard comme les bissectrices des angles droits.
6ème - EVAPM 6/97- Tl :
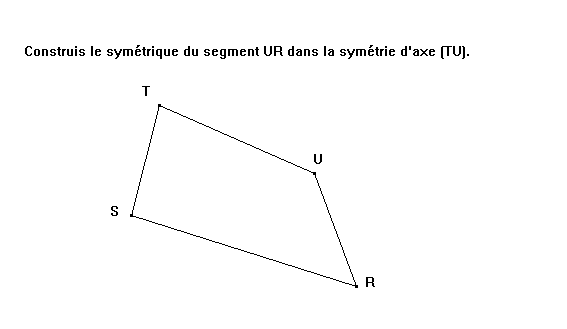
Il s’agit de construire le symétrique du segment [UR] dans la symétrie d’axe (TU).
24 % réussissent et 11% donnent le symétrique du quadrilatère.
3% donnent le symétrique de [TU] dans la symétrie d’axe (UR).
Mais comme dans l’exercice précédent, la lecture de l’énoncé n’est pas facile et l’axe est un côté de la figure.
